This Angular Universal Tutorial explains how to achieve Server Side Rendering using Angular Universal. Server-Side Rendering or SSR is a technique, which renders the pages on the server-side before sending it to the browser. We will learn what is Angular Universal is and the need for server-side rendering. Later we will show you how to create an example angular universal app with server-side rendering. We also discuss the very important things that you should know before you diving into server-side rendering using Angular Universal.
Table of Contents
What is Angular Universal
The Angular Universal renders the HTML view of the requested URL at the server, before sending it to the user’s browser. This will make the app load faster and more importantly search engine friendly.
Why Server Side rendering required
The Angular apps are single-page applications. They consist of lots of javascript code. These Javascript codes run on the client’s browser and generate an HTML view on the fly. The app does not send any request to the server when the user navigates from one page to another page. The Browser does all the renderings of the page. App sends requests only for data & static resources like images to the backend. This makes the app work very fast for the user.
But it is search engines who bring users to the site. They assign ranks to each page based on several factors. Speed & Content are the two of the topmost ranking factors. This is where SPA frameworks like Angular suffer.
Speed
The initial loading of the Angular apps is slow because,
- It needs to download a lot of JavaScript files
- Execute the JavaScript and render the HTML to the view.
Content
To see the content, the search engines need to execute JavaScript. Although Google does a good job of executing the JavaScript and reading the content, you cannot trust it to get it right all the time. The other search engines like bing etc also not able to process it. The social media crawlers like Facebook & twitter do not execute JavaScript, Hence they will not see the content.
We can solve the above problems by rendering the content at the server and send the static HTML to the user.
What is Server-Side Rendering
Server-Side Rendering or SSR is a technique, which executes the javascript and generates the HTML file on the server and sends it to the client-side.
For Example, when the request for a specific page arrives at the server, it locates the index.html. Now instead of sending it to the browser, the server passes it to a renderer process. The Renderer executes the Angular Framework (as if it is running in the browser) and generates the HTML. It also makes HTTP Requests to the backend server if required to get the data. Finally, the server sends the generated HTML to the Browser
The Browser now shows the HTML to the user. At this point the browser is yet to download the Angular, Hence the mouse movements & keyboard events will not have any effect on the page. The page is not yet interactive.
The browser starts to download the Angular framework. Once the Angular loads and bootstraps, it starts to capture the user events. The page becomes interactive. From this point onwards, the Angular takes over & any further navigation happens at client side
Server Side rendering Vs Client-Side Rendering
The following table shows the difference between Server-side rendering Vs Client-Side Rendering.
| Sr.No | Client-Side Rendering | Server Side Rendering |
|---|---|---|
| 1 | User sends the requests for a page | User sends the requests for a page |
| 2 | Server locate the index.html and sends it to the user | Server locate the index.html and sends it to the Renderer Process running in Server |
| 3 | Renderer prepares the initial page, by executing the Angular Framework and sends it to the browser | |
| 4 | The Browser displays the blank page, but there is no content there | The browser shows the initial page to the user. The page may be non-interactive at this time. |
| 5 | The browser downloads the CSS & JavaScript | The browser downloads the CSS & Javascript |
| 6 | Browser executes Angular Framework (JavaScript) & Renders the page | Browser executes Angular Framework (JavaScript) |
| 7 | User sees the Interactive Page | The page becomes interactive. |
Now, let us see how this solves the problem of Content & Speed
Content and SSR
Since the server generates the content, there is no need for search engines to execute the javascript. The social media crawlers also see the HTML
Speed and SSR
Does it solves the problem of speed?. The short answer is NO.
Implementing SSR does not speed up your site all by itself. Because you are only moving the rendering to the server from the browser. In fact, if the server is busy, it may slow your site down.
But it will improve the first contentful paint or FCP.
But, you get a great speed when you cache the rendered response. Serving the cached response to the user eliminates the rendering process and serves the HTML instantly to the user. This is possible only with the SSR.
Angular Universal Tutorial
Create a new Angular project using the Angular CLI
1 2 3 | ng new ssr |
Check the app is running by using the command
1 2 3 | ng serve |
Right-click anywhere on the browser windows and view page source. You will see that there is no content. This is what search engines will see when they crawl your site.
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 | <!doctype html> <html lang="en"> <head> <meta charset="utf-8"> <title>Ssr</title> <base href="/"> <meta name="viewport" content="width=device-width, initial-scale=1"> <link rel="icon" type="image/x-icon" href="favicon.ico"> </head> <body> <app-root></app-root> <script src="runtime.js" type="module"></script><script src="polyfills.js" type="module"></script><script src="styles.js" type="module"></script><script src="vendor.js" type="module"></script><script src="main.js" type="module"></script></body> </html> |
Adding Angular Universal
To add Angular Universal to the above project, run the following command. It will add the express-engine to the project. You should specify the name of the project under the flag --clientProject. Name of the project is what you specify while creating the project using ng new <projectName>
1 2 3 | ng add @nguniversal/express-engine --clientProject ssr |
You can find the project name from the angular.json file from projects node.
1 2 3 4 5 6 7 8 9 10 | { "$schema": "./node_modules/@angular/cli/lib/config/schema.json", "version": 1, "newProjectRoot": "projects", "projects": { "ssr": { ====> Name of the project "projectType": "application", "schematics": {}, |
Now, you can run the project by running the following command
1 2 3 | npm run build:ssr && npm run serve:ssr |
It will take a while to compile it as shown in the image below
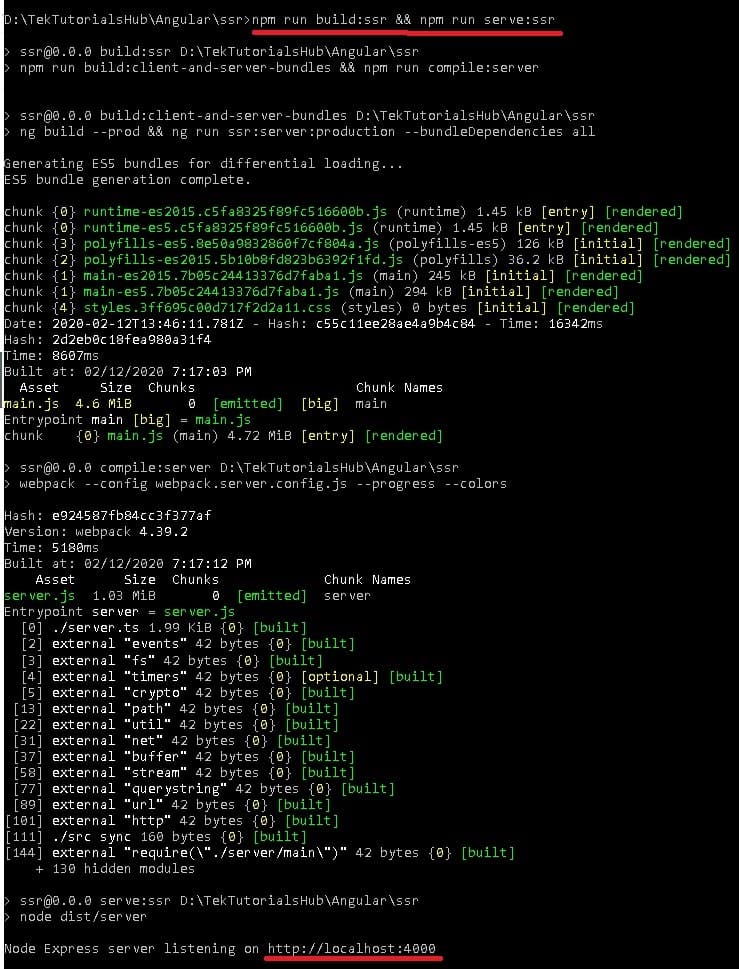
The App will run on the port 4000 instead of 4200. You can now right-click and look at the source and you will see the content. This is what crawlers see when they visit your site.
Things to Note
No Hash Location Strategy
If you are still using HashLocationStrategy (where URL looks like http://localhost:4200/#/product ) then you better move to PathLocationStrategy. They won’t work with Universal Apps.
Browser API Do not work
The objects such as window, location & document, etc work only on the browser. They do not exist on the server. You can make use of Document or Location for those tasks.
If you are manipulating the DOM elements by using the nativeElement of the ElementRef then it will also not work on the server. You can make use of the Renderer2
Find out where you are running server or browser
Sometimes it is necessary to find out whether the code is executing on the server or browser. For instance, you may want to make use of a browser API, which won’t work in the server and may result in an error. The Angular has isPlatformBrowser & isPlatformServer methods from the @angular/common package. You need to inject them using the PLATFORM_ID injection token
The Duplication of HTTP Requests.
Consider the example where your app makes a request to the back end to get some data and displays it to the user.
When the page requests for the data, the server makes the HTTP Request for the data. It waits for the HTTP Request to finish before rendering the page. Then the server sends the page to the browser. The Browser instantly displays the page along with the data.
Now, Browser downloads and bootstraps the Angular framework. The Angular also makes the same HTTP request to get the data, resulting in duplication.
To Mitigate that, you can make use of BrowserTransferStateModule & ServerTransferStateModule.
Make URL’s Absolute
If you are making HTTP requests from the client-side, then ensure that you use absolute URLs. The Requests with Relative URLs fail during the SSR.
HTTP Security
The authenticated HTTP Request for data to the backend server fails in Server. Because the server cannot access the authentication cookies stored in the client. You will have to handle the security at the server-side your self.
Browser Events
SSR Apps sends the rendered HTML to the browser and browser immedialyty displays it. In the backgroud, browser downloads the Angular Framework and then bootstraps it.
In between these two events, the user sees the non-interactive page, because angular is yet to load. The events like clicking on a button or mouse movements are not captured.
You can work around this problem using PreBoot Library It Replays all events once the app becomes interactive. Hence user do not have to perform the actions again
Summary
In this Angular Universal Tutorial, we learned how to implement Server Side Rendering. The SSR is useful when you want your app to be Search engine friendly.



You cannot run this script on the current system. For more information about running scripts and setting execution
policy, see about_Execution_Policies at https:/go.microsoft.com/fwlink/?LinkID=135170
I have an error like this how can i rectify this???
click or selectedTab change events or not working after upgraded the angular10 app to Server side rendering.
Please re check your code. Angular 10 or SSR might not be cause for the error